Polygon Triangulation
A Project by Christopher R. Wicks
for Computational Geometry
Rochester Institute of Technology
Fall 2016 Semester
View the Project on GitHub wickstopher/triangulation
To build and run the project from source, download the above .zip file or tarball and check out the README file. Prerequisites for building the project from include GNU Make, the Java 8 SDK, and Apache Maven.
You can also simply download a prebuilt executable JAR file of the application and run it in the usual way (Java 8 required).
x-monotonicity
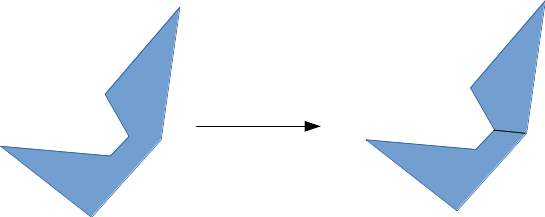
A polygon is said to be x-monotone if for any given vertical line on the plane, that polygon is intersected by that line at most twice. Fun fact: since monotonicity is defined with respect to a given axis, note that the example provided below is not y-monotone. If we were to run the algorithm from, for example, top-to-bottom instead of left-to-right, we would require a y-monotone polygon.


As stated previously, this is a two phase algorithm. The second phase of the algorithm requires monotone polygons as input, so in the first phase we break down an arbitrary closed polygon into monotone polygons.
The process for doing this is by using a sweep-line algorithm with one event per polygon vertex. We literally sweep across the polygon and any time we "bump into" a vertex, we process the event at that vertex.
Vertex Types for Event Processing
- Split: Vertex is the left endpoint of both of its incident edges, and its interior angle is greater than π
- Merge: Vertex is the right endpoint of both of its incident edges, and its interior angle is greater than π
- Start: Vertex is the left endpoint of both of its incident edges, and its interior angle is less than π
- End: Vertex is the right endpoint of both of its incident edges, and its interior angle is less than π
- Upper: Given a counter-clockwise orientation, the vertex is the right endpoint of its "next" edge and the left endpoint of its "previous" edge
- Lower: Given a counter-clockwise orientation, the vertex is the right endpoint of its "previous" edge and the left endpoint of its "next" edge
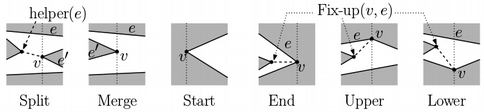
image source: David Mount's Lecture Notes for Computational Geometry
Monotone Polygon Subdivision Algorithm
First, we define Fix-up(v,e) as follows: if helper(e) is a merge vertex, add a diagonal from v to helper(e).
Recall too that the event vertices are in a list sorted by x-coordinate.
For each event vertex, v:
- If v is a split vertex: let e be the edge on the sweep-line immediately above v and add a diagonal connecting v to helper(e). Let e’ be the v’s lower incident edge. Make v the helper of both e and e’. Add v’s incident edges to the sweep-line status.
- If v is a merge vertex: delete its incident edges from the sweep-line status. Let e be the edge now lying immediately above v on the sweep-line. Let e’ be v’s lower incident edge. Fix-up(v,e) and Fix-up(v,e’). Make v the helper of e. *
- If v is an end vertex: delete its adjacent edges from the sweep-line status. Let e be v’s upper incident edge. Fix-up(v,e).
- If v is an upper vertex: let e be v’s left incident edge. Fix-up(v,e). Delete e from the sweep-line status and add v’s right incident edge. Make v the helper of its right incident edge.
- If v is a lower vertex: let e be the edge above v on the sweep-line status. Fix-up(v,e). Delete v’s left incident edge from the sweep-line status and add v’s right incident edge. Make v the helper of its right incident edge.
* This detail was missing from the algorithm source, but is crucial for the algorithm to function correctly
Algorithm source: David Mount's Lecture Notes for Computational Geometry.
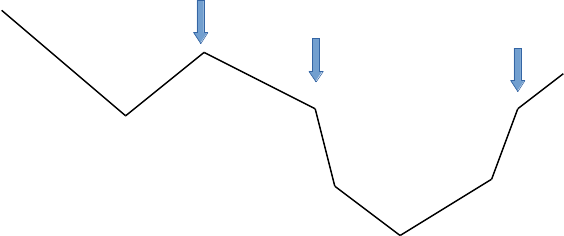
Event Types for Polygon Triangulation
Now that we have subdivided our polygon into monotone polygons, we can use the next phase of the algorithm to triangulate each polygon individually! Much like with our previous sweep-line algorithm, there is only one event per polygon vertex, and they are sorted from left-to-right by x-coordinate. The event type for this algorithm is a little simpler, but like the previous algorithm corresponds to the vertex's location on the polygon:
- The leftmost vertex (there can only be one!)
- The rightmost vertex (again, only one!)
- An upper-chain vertex
- A lower-chain vertex
Monotone Polygon Triangulation
A given vertex on a monotone polygonal curve is said to be a "reflex" vertex if its interior angle is greater than π.
For each vertex following the leftmost vertex, let vi be that vertex and let vi-1 be the vertex associated with the previous event. We maintain a stack uf untriangulated vertices.
- If vi and vi-1 lie on opposite chains, we add diagonals between vi and the untriangulated vertices on the opposing stack.
- If vi and vi-1 lie on the same chain, there are two cases:
- If vi-1 is a reflex vertex, that means that none of the prior vertices on the reflex chain are visible to vi, so we simply add vi to the chain.
- If vi-1 is a non-reflex vertex, we pop vertices off the reflex chain that are visible to vi-1, adding diagonals between vi-1 and each of those vertices, leaving the last remaining visible vertex on the chain.
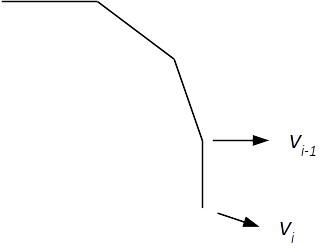
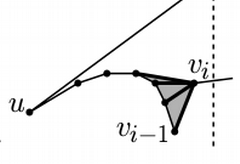
image source: David Mount's Lecture Notes for Computational Geometry